HESI Math Test Prep
If you are serious about getting a great score on your HESI math test, try out our recommended HESI Math Prep Course.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Subtract: 1001 − 99 =
900 | |
902 | |
999 | |
1,000 |
Question 1 Explanation:
Count up from 99 to 100 (+1) and from 100 to 1001 (+901). The answer is the sum of 901 and 1.
Question 2 |
What is 70% of 65?
45.5 | |
50.5 | |
65 | |
110.5 |
Question 2 Explanation:
Recall that:
$\dfrac{\text{part}}{\text{whole}} = \dfrac{\%}{100}$
Substitute given values and solve for the unknown:
$\dfrac{x}{65} = \dfrac{75}{100}$
$(x)(100) = (65)(70)$
$100x = 4550$
$x = 45.50$
Alternatively, directly multiplying 65 by 0.7 will yield the same result.
$\dfrac{\text{part}}{\text{whole}} = \dfrac{\%}{100}$
Substitute given values and solve for the unknown:
$\dfrac{x}{65} = \dfrac{75}{100}$
$(x)(100) = (65)(70)$
$100x = 4550$
$x = 45.50$
Alternatively, directly multiplying 65 by 0.7 will yield the same result.
Question 3 |
For a recipe, there are 3 eggs needed for every pound of cake needed. How many pounds of cake can be made if there are 40 eggs? Round to the nearest pound.
12 | |
13 | |
14 | |
15 |
Question 3 Explanation:
Write a proportion to represent the situation:
$\dfrac{3 \text{ eggs}}{1 \text{ cake}} = \dfrac{40 \text{ eggs}}{x \text{ cakes}}$
Cross multiply and solve for the variable $x$:
3$x$ = 40 → $x$ = 13$\frac{1}{3}$
Only 13 pounds of cake can be made.
$\dfrac{3 \text{ eggs}}{1 \text{ cake}} = \dfrac{40 \text{ eggs}}{x \text{ cakes}}$
Cross multiply and solve for the variable $x$:
3$x$ = 40 → $x$ = 13$\frac{1}{3}$
Only 13 pounds of cake can be made.
Question 4 |
Evaluate:
$x^4 − y$ if $x$ = 3 and $y$ = 20
$x^4 − y$ if $x$ = 3 and $y$ = 20
61 | |
65 | |
−8 | |
−10 |
Question 4 Explanation:
Substitute the values of $x$ and $y$ into the given equation and evaluate:
= 34 − (20)
= 3×3×3×3 − (20)
= 81 − 20
= 61
= 34 − (20)
= 3×3×3×3 − (20)
= 81 − 20
= 61
Question 5 |
A large clinic administers 1136 doses of vaccine over the course of 16.8 hours. How many doses per hour did the clinic administer? Round to the nearest whole number.
68 | |
69 | |
70 | |
67 |
Question 5 Explanation:
We need to divide 1136 doses by 16.8 hours.
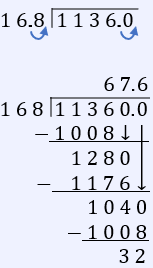
Note: Since we are rounding to the nearest whole number, we need to calculate our answer to one decimal point.
67.6 rounded to the nearest whole number is 68.

Note: Since we are rounding to the nearest whole number, we need to calculate our answer to one decimal point.
67.6 rounded to the nearest whole number is 68.
Question 6 |
Add: 9.43 + 11.3 =
21.73 | |
10.7 | |
20.73 | |
25.85 |
Question 6 Explanation:
Vertically align the numbers so that the decimals are on top of each other:
$\begin{align} 9.43& \\ \underline{+\quad 11.30}& \\ 20.73& \end{align}$
$\begin{align} 9.43& \\ \underline{+\quad 11.30}& \\ 20.73& \end{align}$
Question 7 |
Multiply: (226)(55.3) =
24,277.3 | |
12,497.8 | |
32,449.3 | |
11,936.5 |
Question 7 Explanation:
To multiply decimals, line up the numbers on the right (do not align the decimal points). Then starting on the right, multiply each digit of the top number by each digit of the bottom number. Then add the products:
$\begin{align} 226& \\ \underline{×\quad 55.3}& \\ 678 \\ 1130 \phantom{0} \\ \underline{+\quad 1130\phantom{00}}& \\ 124978& \end{align}$
Once you have added the products, you must place the decimal point correctly. There are zero decimal places in 226 and one decimal place in 55.3, which gives us a total of one decimal place. Starting at the right of our answer move one place to the left and put the decimal point there:
$12{,}497.8$
$\begin{align} 226& \\ \underline{×\quad 55.3}& \\ 678 \\ 1130 \phantom{0} \\ \underline{+\quad 1130\phantom{00}}& \\ 124978& \end{align}$
Once you have added the products, you must place the decimal point correctly. There are zero decimal places in 226 and one decimal place in 55.3, which gives us a total of one decimal place. Starting at the right of our answer move one place to the left and put the decimal point there:
$12{,}497.8$
Question 8 |
How many millimeters are there in 5 meters?
500 | |
5,000 | |
50,000 | |
500,00 |
Question 8 Explanation:
The prefix “milli-” means 1,000. There are 1,000 millimeters in 1 meter, so there are 5,000 millimeters in 5 meters. Alternatively, use dimensional analysis to convert:
$5 \text{ m} \ast \frac{100 \text{ cm}}{1 \text{ m}} \ast \frac{10 \text{ mm}}{1 \text{ cm}}$ $ = 5000 \text{ mm}$
$5 \text{ m} \ast \frac{100 \text{ cm}}{1 \text{ m}} \ast \frac{10 \text{ mm}}{1 \text{ cm}}$ $ = 5000 \text{ mm}$
- 1 Kilometer = 1,000 Meters
- 1 Meter = 100 Centimeters
- 1 Centimeter = 10 Millimeters
Question 9 |
Which of the following is equivalent to 0.0009?
0.0009% | |
0.009% | |
0.09% | |
0.9% |
Question 9 Explanation:
In order to convert a decimal to a percent you need to move the decimal point two places to the right and add the percent symbol. This is equivalent to dividing the original value by 100.
Question 10 |
Multiply: $\, \dfrac{5}{8} × \dfrac{2}{9} =$
Express your answer in the simplest form.
Express your answer in the simplest form.
$\dfrac{7}{72}$ | |
$\dfrac{7}{36}$ | |
$\dfrac{1}{13}$ | |
$\dfrac{5}{36}$ |
Question 10 Explanation:
$\dfrac{5}{8} × \dfrac{2}{9}$
When multiplying, there is no need to find a common denominator.
$\dfrac{5 × 2}{8 × 9} = \dfrac{10}{72} = \dfrac{5}{36}$
When multiplying, there is no need to find a common denominator.
$\dfrac{5 × 2}{8 × 9} = \dfrac{10}{72} = \dfrac{5}{36}$
Question 11 |
Convert the following military time to regular time:
15:17:52 hours
15:17:52 hours
5:17:52 AM | |
5:17:52 PM | |
3:17:52 AM | |
3:17:52 PM |
Question 11 Explanation:
For a military time that's 13 hours or higher, simply subtract 12 hours to get the standard time. Also, since the military time in this case starts higher than 12 hours, we know that it is PM.
Question 12 |
Add: $\, \dfrac{3}{7} + \dfrac{2}{3} =$
$\dfrac{25}{21}$ | |
$\dfrac{23}{21}$ | |
$\dfrac{27}{21}$ | |
$\dfrac{19}{21}$ |
Question 12 Explanation:
When adding fractions, we first need to find a common denominator.
$\dfrac{3}{7} + \dfrac{2}{3}$
The smallest number that both 7 and 3 go into is 21.
$\dfrac{3 × 3}{7 × 3} + \dfrac{2 × 7}{3 × 7}$
$\dfrac{9}{21} + \dfrac{14}{21}$
$\dfrac{23}{21}$
$\dfrac{3}{7} + \dfrac{2}{3}$
The smallest number that both 7 and 3 go into is 21.
$\dfrac{3 × 3}{7 × 3} + \dfrac{2 × 7}{3 × 7}$
$\dfrac{9}{21} + \dfrac{14}{21}$
$\dfrac{23}{21}$
Question 13 |
Solve the proportion (find the value of $x$):
$9:14 \; :: \; x:56$
$9:14 \; :: \; x:56$
$x$ = 14 | |
$x$ = 25 | |
$x$ = 36 | |
$x$ = 42 |
Question 13 Explanation:
The first step to solving a proportion problem is to rewrite the problem as a fraction.
$\dfrac{9}{14} = \dfrac{x}{56}$
Then you cross-multiply and solve the resulting equation.
14$x$ = (9)(56)
14$x$ = 504
$x$ = $\frac{504}{14}$
$x$ = 36
$\dfrac{9}{14} = \dfrac{x}{56}$
Then you cross-multiply and solve the resulting equation.
14$x$ = (9)(56)
14$x$ = 504
$x$ = $\frac{504}{14}$
$x$ = 36
Question 14 |
Divide: $\, \dfrac{2}{5} ÷ \dfrac{3}{7} =$
$\dfrac{6}{35}$ | |
$\dfrac{14}{35}$ | |
$\dfrac{11}{15}$ | |
$\dfrac{14}{15}$ |
Question 14 Explanation:
$\dfrac{2}{5} ÷ \dfrac{3}{7}$
When dividing fractions, multiply by the reciprocal of the second fraction.
$\dfrac{2}{5} × \dfrac{7}{3} = \dfrac{2 × 7}{5 × 3} = \dfrac{14}{15}$
When dividing fractions, multiply by the reciprocal of the second fraction.
$\dfrac{2}{5} × \dfrac{7}{3} = \dfrac{2 × 7}{5 × 3} = \dfrac{14}{15}$
Question 15 |
Joe makes \$20 an hour and Tim makes \$30 an hour. How many hours more than Tim must Joe work to earn the same amount Tim makes in 4 hours?
1 | |
2 | |
3 | |
4 |
Question 15 Explanation:
Tim will make \$120 in 4 hours and Joe will need 6 hours to make \$120. So 6 − 4 = 2
Question 16 |
Solve for x:
3(x − 4) = 18
3(x − 4) = 18
x = 3/2 | |
x = 22/3 | |
x = 6 | |
x = 10 |
Question 16 Explanation:
This is a basic algebra problem where you are need to solve for a variable. To solve this, first divide both sides by 3:
3(x − 4) = 18
x − 4 = 18/3
x − 4 = 6
Then solve for x:
x − 4 = 6
x = 6 + 4
x = 10
3(x − 4) = 18
x − 4 = 18/3
x − 4 = 6
Then solve for x:
x − 4 = 6
x = 6 + 4
x = 10
Question 17 |
There are 6,657 marbles in a jar. Approximately 34% are white, and the rest are black. How many black marbles are there?
2,263 | |
4,394 | |
1,098 | |
66 |
Question 17 Explanation:
If 34% of the marbles are white, then 66% must be black.
(0.66)(6,657) = 4,393.62
(0.66)(6,657) = 4,393.62
Question 18 |
At a comic book store, Robert purchased three comics for \$2.65 each. If he paid with a \$20 bill, how much change did he receive?
$12.05 | |
$13.15 | |
$13.85 | |
$17.35 |
Question 18 Explanation:
Three comics at \$2.65 would equal a total of \$7.95. The change would equal \$20 − \$7.95 = \$12.05.
Question 19 |
What is the boiling point of water?
32° Fahrenheit | |
100° Fahrenheit | |
100° Celsius | |
212° Celsius |
Question 19 Explanation:
The boiling point of water is 100° Celsius or 212° Fahrenheit.
The freezing point of water is 0° Celsius or 32° Fahrenheit.
The freezing point of water is 0° Celsius or 32° Fahrenheit.
Question 20 |
A patient is receiving pain relief via a 1000 ml IV bag solution. When the patient has received 300 ml of the IV solution, they have received 2.1 mg of morphine.
How many milligrams of morphine were contained in the original 1000 ml IV bag?
(If rounding is necessary, round to the nearest tenth.)
(If rounding is necessary, round to the nearest tenth.)
6.3 mg | |
6.7 mg | |
7.7 mg | |
7.0 mg |
Question 20 Explanation:
Start by setting up a proportion:
$\dfrac{2.1 \text{ mg}}{300 \text{ ml}} = \dfrac{x \text{ mg}}{1000 \text{ ml}}$
$(2.1)(1000) = (300)(x)$
$2100 = 300x$
$x = \dfrac{2100}{300} = \dfrac{21}{3}$
$x = 7$
7.0 mg of morphine was contained in the original bag.
$\dfrac{2.1 \text{ mg}}{300 \text{ ml}} = \dfrac{x \text{ mg}}{1000 \text{ ml}}$
$(2.1)(1000) = (300)(x)$
$2100 = 300x$
$x = \dfrac{2100}{300} = \dfrac{21}{3}$
$x = 7$
7.0 mg of morphine was contained in the original bag.
Question 21 |
Subtract: 8,674.5 − 998.9 =
4,445.67 | |
7,675.6 | |
8,294.6 | |
3,349.5 |
Question 21 Explanation:
This subtraction problem requires regrouping (borrowing).


Question 22 |
Add: 1.332 + 0.067
2.139 | |
1.453 | |
1.399 | |
1.378 |
Question 22 Explanation:
Vertically align the numbers so that the decimals are on top of each other:
$\begin{align} 1.332& \\ \underline{+\quad 0.067}& \\ 1.399& \end{align}$
$\begin{align} 1.332& \\ \underline{+\quad 0.067}& \\ 1.399& \end{align}$
Question 23 |
Multiply: (44.44)(55.55) =
Round to the nearest hundredth.
Round to the nearest hundredth.
2,467.64 | |
2,468.64 | |
3,000.46 | |
155.00 |
Question 23 Explanation:

The decimal is moved four places to the left because we have a total of four places after the decimal in the two numbers being multiplied together.
Question 24 |
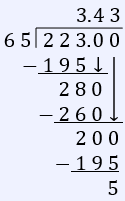
Divide: 223 ÷ 65 =
5.1 | |
3.4 | |
2.3 | |
1.2 |
Question 24 Explanation:
This problem can be solved using long division:

Question 25 |
Dosing instructions for a prescription oral pain medicine call for 0.4 milligrams per kilogram of body weight 2 times per day. If a patient is taking a total dosage of 44.8
mg/day, what is the patient’s weight in kilograms?
Round to the nearest kilogram.
Round to the nearest kilogram.
50 kg | |
52 kg | |
47 kg | |
56 kg |
Question 25 Explanation:
44.8 mg/day means they are taking:
$\dfrac{44.8 \text{ mg/day}}{2 \text{ doses/day}} = 22.4 \dfrac{\text{mg}}{\text{dose}}$ (22.4 mg twice each day)
$(0.4 \text{ mg/kg})(x \text{ kg}) $ $ = 22.4 \text{ mg}$
$0.4x = 22.4$
$x = \dfrac{22.4}{0.4}$
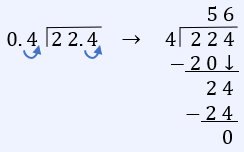
$x = 56$
$\dfrac{44.8 \text{ mg/day}}{2 \text{ doses/day}} = 22.4 \dfrac{\text{mg}}{\text{dose}}$ (22.4 mg twice each day)
$(0.4 \text{ mg/kg})(x \text{ kg}) $ $ = 22.4 \text{ mg}$
$0.4x = 22.4$
$x = \dfrac{22.4}{0.4}$

$x = 56$
Question 26 |
A rat can finish a maze in about 3 minutes. If a small backpack is put on the rat so it reduces its speed by 50%, how much longer will it take the rat to finish the maze?
3 minutes | |
6 minutes | |
10 minutes | |
12 minutes |
Question 26 Explanation:
If the rat's speed is reduced by 50%, then it will take the rat twice as long, or 6 minutes. This is 3 minutes longer than it took before.
Question 27 |
A nurse's schedule is written in military time, and shows their shift is from 1500 to 0100. When will they get off work?
Noon | |
Early afternoon | |
Just before midnight | |
A little bit after midnight |
Question 27 Explanation:
Converted to regular time, their schedule is 3:00 PM to 1:00 AM. So they will get off at 1:00 AM, which is a little bit after midnight.
Question 28 |
Convert 26° Celsius to Fahrenheit.
−3.3° F | |
−6° F | |
46.8° F | |
78.8° F |
Question 28 Explanation:
To convert from Celsius to Fahrenheit you can use this formula:
(°C × 9/5) + 32 = °F
Or you can just follow these steps:
1) Multiply by 9
2.) Divide by 5
3.) Add 32
(°C × 9/5) + 32 = °F
Or you can just follow these steps:
1) Multiply by 9
2.) Divide by 5
3.) Add 32
Question 29 |
The probability of a side effect occurring is 0.15. How would this decimal be written as a fraction? Be sure to write in its simplest form.
$\dfrac{1}{7}$ | |
$\dfrac{4}{45}$ | |
$\dfrac{2}{15}$ | |
$\dfrac{3}{20}$ |
Question 29 Explanation:
The decimal 0.15 can be written as fifteen hundredths. Then simplify as shown:
$0.15 = \dfrac{15}{100} = \dfrac{3}{20}$
$0.15 = \dfrac{15}{100} = \dfrac{3}{20}$
Question 30 |
Multiply: (0.67)(0.09) =
0.000603 | |
0.006030 | |
0.060300 | |
0.603000 |
Question 30 Explanation:
The product of two decimals will always have the same number of decimal places as the sum of the number of decimal places that the multiplicand and the multiplier have.
(67)(9) = 603. The multiplicand is .67 and has 2 decimal places. The multiplier is .09 and has 2 decimal places. Our product should have 4 decimal places. Therefore, our answer is .0603. Don't get tripped up by the extra zeros. Zeros before our answer and after the decimal point increase the number of decimal places. Zeros after our answer and after the decimal point do not increase the number of decimal places.
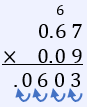
(67)(9) = 603. The multiplicand is .67 and has 2 decimal places. The multiplier is .09 and has 2 decimal places. Our product should have 4 decimal places. Therefore, our answer is .0603. Don't get tripped up by the extra zeros. Zeros before our answer and after the decimal point increase the number of decimal places. Zeros after our answer and after the decimal point do not increase the number of decimal places.

Question 31 |
A nurse working at a medical clinic earns \$17.81 per hour. The nurse works three 8-hour shifts and one 12-hour shift every week, and is paid weekly. Weekly deductions are: federal tax \$102.80, state tax \$24.58, federal insurance \$18.13, and family health insurance \$52.15. What is the nurse's take-home pay each week?
$158.54 | |
$443.50 | |
$514.74 | |
$641.16 |
Question 31 Explanation:
First you must calculate how many hours the nurse works each week. Three 8-hour shifts plus one 12-hour shift equals 36 hours per week.
Beginning Salary = 36 × \$17.81 = \$641.16
Deductions = \$102.80 + \$24.58 + \$18.13 + \$52.15 = \$197.66
Take-Home Pay = \$641.16 − \$197.66 = \$443.50
Beginning Salary = 36 × \$17.81 = \$641.16
Deductions = \$102.80 + \$24.58 + \$18.13 + \$52.15 = \$197.66
Take-Home Pay = \$641.16 − \$197.66 = \$443.50
Question 32 |
There are 48 students studying foreign language at the community college. The only two foreign languages offered are French and Spanish, and a student cannot take both. If 28 students are studying French, which of the following represents the ratio of students studying Spanish to the total number of foreign language students?
2/7 | |
1/2 | |
1/3 | |
5/12 |
Question 32 Explanation:
If there are 48 total, and 28 study French, then 20 study Spanish. The ratio of 20 to 48 = 20/48 = 10/24 = 5/12.
Question 33 |
Express the improper fraction $\dfrac{81}{7}$ as a whole number with decimal. Round to the nearest tenth.
11.6 | |
11.1 | |
10.8 | |
10.3 |
Question 33 Explanation:
$\dfrac{81}{7}$
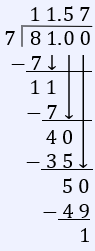
Note: Since rounding to 1 decimal place we calculate our answer to 2 decimal places.
11.57 rounded to the nearest tenth = 11.6
Question 34 |
A patient has a height of 1.6 meters and a weight of 67 kilograms. What is the patient’s BMI (Body Mass Index)?
Use the formula: BMI = mass/height2 where the mass is in kilograms and the height is in meters. (Note: the height is squared in the BMI formula.)
Round to the nearest whole number.
Use the formula: BMI = mass/height2 where the mass is in kilograms and the height is in meters. (Note: the height is squared in the BMI formula.)
Round to the nearest whole number.
28 kg/m2 | |
26 kg/m2 | |
30 kg/m2 | |
24 kg/m2 |
Question 34 Explanation:
Plug the given numbers into the given formula and then calculate:
$\text{BMI} = \dfrac{\text{mass}}{\text{height}^2} =\dfrac{67}{1.6^2}$
$1.6^2 = (1.6)(1.6) = 2.56$
$\text{BMI} = \dfrac{67}{2.56}$

$\text{BMI} = 26\dfrac{\text{kg}}{\text{m}^2}$
$\text{BMI} = \dfrac{\text{mass}}{\text{height}^2} =\dfrac{67}{1.6^2}$
$1.6^2 = (1.6)(1.6) = 2.56$
$\text{BMI} = \dfrac{67}{2.56}$

$\text{BMI} = 26\dfrac{\text{kg}}{\text{m}^2}$
Question 35 |
Add: $\,2\dfrac{1}{8} + 1\dfrac{5}{9}$
$2\dfrac{53}{72}$ | |
$2\dfrac{43}{72}$ | |
$3\dfrac{47}{72}$ | |
$3\dfrac{49}{72}$ |
Question 35 Explanation:
First convert the mixed fractions to improper fractions. Then find a common denominator in order to add:
$2\dfrac{1}{8} + 1\dfrac{5}{9}$
$\dfrac{17}{8} + \dfrac{14}{9}$
$\dfrac{9}{9} \cdot \dfrac{17}{8} + \dfrac{8}{8} \cdot \dfrac{14}{9}$
$\dfrac{153}{72} + \dfrac{112}{72}$
$\dfrac{265}{72}$
Now convert back to a mixed fraction:
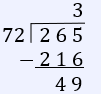
$3\dfrac{49}{72}$
$2\dfrac{1}{8} + 1\dfrac{5}{9}$
$\dfrac{17}{8} + \dfrac{14}{9}$
$\dfrac{9}{9} \cdot \dfrac{17}{8} + \dfrac{8}{8} \cdot \dfrac{14}{9}$
$\dfrac{153}{72} + \dfrac{112}{72}$
$\dfrac{265}{72}$
Now convert back to a mixed fraction:
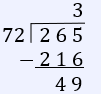
$3\dfrac{49}{72}$
Question 36 |
A 0.75% NaCl (Sodium Chloride) solution contains 0.75 mg of NaCl per 100 ml of solution. How many milligrams of NaCl would be contained in 3 liters of the solution? Round your answer to the nearest tenth of a milligram.
20.5 mg | |
23.0 ml | |
22.5 mg | |
21.0 ml |
Question 36 Explanation:
$\require{cancel} 3 \cancel{\text{liters}} \cdot \dfrac{1000 \text{ ml}}{1 \cancel{\text{liter}}} = 3000 \text{ ml}$
$\dfrac{0.75 \text{ mg}}{100 \text{ ml}} = \dfrac{x \text{ mg}}{3000 \text{ ml}}$
$(0.75)(3000) = (100)(x)$
$x = \dfrac{(0.75)(3000)}{(100)}$ $\quad$ $\frac{3000}{100} = \frac{30}{1} = 30$
$x=(0.75)(30)$
$x=22.5$
Question 37 |
If each tablet contains 230 mg of glucose, how many milligrams of this ingredient will there be in 75 tablets?
18,100 mg | |
18,750 mg | |
17,550 mg | |
17,250 mg |
Question 37 Explanation:
We need to multiply 230 by 75 to determine the total milligrams:
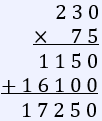
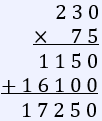
Question 38 |
Subtract: $\,\dfrac{2}{3} − \dfrac{3}{7}$
$\dfrac{9}{21}$ | |
$\dfrac{3}{21}$ | |
$\dfrac{7}{21}$ | |
$\dfrac{5}{21}$ |
Question 38 Explanation:
To subtract fractions, we need a common denominator. The smallest number that both 3 and 7 go into is 21.
$\dfrac{2}{3} − \dfrac{3}{7}$
$\dfrac{7}{7} \cdot \dfrac{2}{3} − \dfrac{3}{3} \cdot \dfrac{3}{7}$
$\dfrac{14}{21} − \dfrac{9}{21}$
$\dfrac{5}{21}$
$\dfrac{2}{3} − \dfrac{3}{7}$
$\dfrac{7}{7} \cdot \dfrac{2}{3} − \dfrac{3}{3} \cdot \dfrac{3}{7}$
$\dfrac{14}{21} − \dfrac{9}{21}$
$\dfrac{5}{21}$
Question 39 |
Divide: 4.6 ÷ 0.3 =
(If rounding is necessary, round to the nearest tenth.)
(If rounding is necessary, round to the nearest tenth.)
14.3 | |
15.3 | |
14.7 | |
13.7 |
Question 39 Explanation:
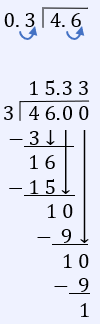
Note: If rounding to the nearest tenth (one decimal place), we need to calculate our answer to two decimal places.
15.33 rounded to the nearest tenth = 15.3
Question 40 |
What is $\dfrac{3}{16}$ of $\dfrac{8}{9}$?
$\dfrac{7}{16}$ | |
$\dfrac{1}{6}$ | |
$\dfrac{11}{144}$ | |
$\dfrac{11}{16}$ |
Question 40 Explanation:
When you see the word "of," think "multiply."
$\dfrac{3}{16} \text{ of } \dfrac{8}{9} = \dfrac{3}{16} × \dfrac{8}{9}$
$= \dfrac{3 × 8}{16 × 9} = \dfrac{24}{144}$
$= \dfrac{2}{12} = \dfrac{1}{6}$
$\dfrac{3}{16} \text{ of } \dfrac{8}{9} = \dfrac{3}{16} × \dfrac{8}{9}$
$= \dfrac{3 × 8}{16 × 9} = \dfrac{24}{144}$
$= \dfrac{2}{12} = \dfrac{1}{6}$
Question 41 |
A prescription medicine has a dosage of 0.6 mg/kg/day divided into three doses per day. If a patient weighs 90 kg, how many milligrams of the medicine would be prescribed per dose? Round to the nearest milligram.
18 mg/dose | |
21 mg/dose | |
24 mg/dose | |
22 mg/dose |
Question 41 Explanation:
$(0.6 \text{ mg/kg/day})(90 \text{ kg}) $ $= 54 \text{ mg/day}$
$\require{cancel} \dfrac{54 \text{ mg}}{ \cancel{\text{day}}} \cdot \dfrac{1 \cancel{\text{day}}}{3 \text{ doses}} $ $ = \dfrac{54 \text{ mg}}{3 \text{ doses}} = 18 \text{ mg/dose}$
Question 42 |
Divide: $\, 10 ÷ 3 \frac{1}{8} =$
$\dfrac{29}{7}$ | |
$\dfrac{27}{8}$ | |
$\dfrac{16}{5}$ | |
$\dfrac{19}{6}$ |
Question 42 Explanation:
First convert the mixed fraction to an improper fraction. Remember that dividing a fraction is the same as multiplying by its reciprocal.
$10 \div 3\frac{1}{8}$
$\dfrac{10}{1} \div \dfrac{25}{8}$
$\dfrac{10}{1} \cdot \dfrac{8}{25} =\dfrac{80}{25} = \dfrac{16}{5}$
$10 \div 3\frac{1}{8}$
$\dfrac{10}{1} \div \dfrac{25}{8}$
$\dfrac{10}{1} \cdot \dfrac{8}{25} =\dfrac{80}{25} = \dfrac{16}{5}$
Question 43 |
Express 65% as a fraction in its simplest form.
$\dfrac{2}{3}$ | |
$\dfrac{11}{14}$ | |
$\dfrac{26}{37}$ | |
$\dfrac{13}{20}$ |
Question 43 Explanation:
A percentage is a number expressed as a fraction of 100:
$65\% = \dfrac{65}{100} = \dfrac{13}{20}$
$65\% = \dfrac{65}{100} = \dfrac{13}{20}$
Question 44 |
Sandy consumes 13,300 calories over the course of 7 days. How many calories does she consume each day on average?
1,700 | |
1,900 | |
2,100 | |
2,300 |
Question 44 Explanation:
We need to divide 13,300 calories by 7 days:
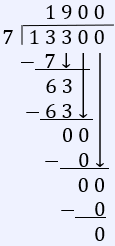
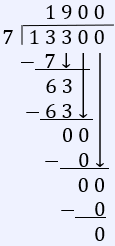
Question 45 |
A patient took 15 ml of medicine 4 times per day for 14 days. In total, how many milliliters of medicine did they take?
870 ml | |
900 ml | |
860 ml | |
840 ml |
Question 45 Explanation:
$\require{cancel} \dfrac{15 \text{ ml}}{\cancel{\text{dose}}} \cdot \dfrac{4 \cancel{\text{doses}}}{\cancel{\text{day}}} \cdot 14 \cancel{\text{days}} $ $ = 840 \text{ ml}$
Question 46 |
Subtract: $\, 5 \frac{2}{7} − 3 \frac{5}{6}$
$1 \frac{13}{42}$ | |
$2 \frac{1}{42}$ | |
$1 \frac{19}{42}$ | |
$1 \frac{11}{42}$ |
Question 46 Explanation:
First convert the mixed fractions to imroper fractions. Then find a common denominator in order to subtract:
$5 \frac{2}{7} − 3 \frac{5}{6}$
$\dfrac{37}{7} − \dfrac{23}{6}$
$\dfrac{6}{6} \cdot \dfrac{37}{7} − \dfrac{7}{7} \cdot \dfrac{23}{6}$
$\dfrac{222}{42} − \dfrac{161}{42}$
$\dfrac{61}{42}$
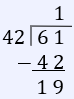
$1 \frac{19}{42}$
$5 \frac{2}{7} − 3 \frac{5}{6}$
$\dfrac{37}{7} − \dfrac{23}{6}$
$\dfrac{6}{6} \cdot \dfrac{37}{7} − \dfrac{7}{7} \cdot \dfrac{23}{6}$
$\dfrac{222}{42} − \dfrac{161}{42}$
$\dfrac{61}{42}$
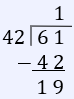
$1 \frac{19}{42}$
Question 47 |
An IV solution is set for a certain number of drops per minute. There are 15 drops per milliliter of IV solution. Over the course of 5 hours, 600 milliliters of the IV solution is delivered? How many drops per minute is the IV delivering?
20 drops/min | |
25 drops/min | |
30 drops/min | |
35 drops/min |
Question 47 Explanation:
$\require{cancel} \dfrac{600 \text{ ml}}{5\cancel{\text{hr}}} \cdot \dfrac{1 \cancel{\text{hr}}}{60 {\text{ min}}} $ $ = \dfrac{600 \text{ ml}}{300 \text{ min}} = 2 \dfrac{\text{ml}}{\text{min}}$
$2 \dfrac{\cancel{\text{ml}}}{{\text{min}}} \cdot \require{cancel} \dfrac{15 \text{ drops}}{1\cancel{\text{ml}}} $ $ = 30 \dfrac{\text{drops}}{\text{min}}$
Question 48 |
An inpatient received a certain dosage of a drug on Wednesday. The dosage was decreased by 20% on Thursday. If the patient received 464 milligrams of the drug on Thursday, what was the dosage received on Wednesday? Round your answer to the nearest milligram.
500 mg | |
540 mg | |
620 mg | |
580 mg |
Question 48 Explanation:
If the dosage was decreased by 20% , then the Thursday dose was 80% (100%−20%) of the Wednesday dose.
80% of Wednesday dose = Thursday dose:
$(0.80)(x) = 464$
$x = \dfrac{464}{0.80}$
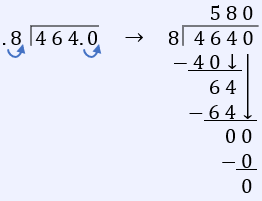
Wednesday dose = 580 mg
80% of Wednesday dose = Thursday dose:
$(0.80)(x) = 464$
$x = \dfrac{464}{0.80}$
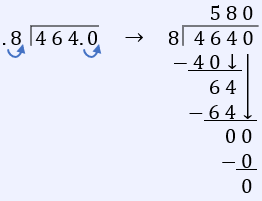
Wednesday dose = 580 mg
Question 49 |
At our hospital, 11 out of the 15 nursing staff are LPNs. How could this be represented as a decimal? (If rounding is necessary, round to the nearest hundredth.)
0.66 | |
0.73 | |
0.81 | |
0.79 |
Question 49 Explanation:
$\dfrac{11}{15}$

Note: Since rounding to two decimal places, we need to calculate our answer to 3 decimal places.
0.733 rounded to the nearest hundredth is 0.73
Question 50 |
Insulin is being dosed at 1.5 units per kilogram per day. If a patient weighs 160 pounds, how much insulin will they use over the course of one year. There are 0.45 kilograms per pound and 365 days per year.
39,420 units | |
43,040 units | |
41,630 units | |
40,280 units |
Question 50 Explanation:
$\require{cancel} 160 \cancel{\text{lbs}} × \dfrac{0.45 \text{ kg}}{\cancel{\text{lb}}} = 72 \text{ kg}$
$(1.5 \text{ units/kg/day})(72 \text{ kg}) $ $ = 108\text{ units/day}$
$\require{cancel} \dfrac{108 \text{ units}}{\cancel{\text{day}}} \cdot \dfrac{365 \cancel{\text{days}}}{1 {\text{ yr}}} $ $ = 39{,}240 \dfrac{\text{units}}{\text{yr}}$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 50 questions to complete.
|
List |
